AngleSD
Forfatter:
ImJaviPerez@gmail.com
Sidst opdateret:
6 år siden
Licens:
Creative Commons CC BY 4.0
Resumé:
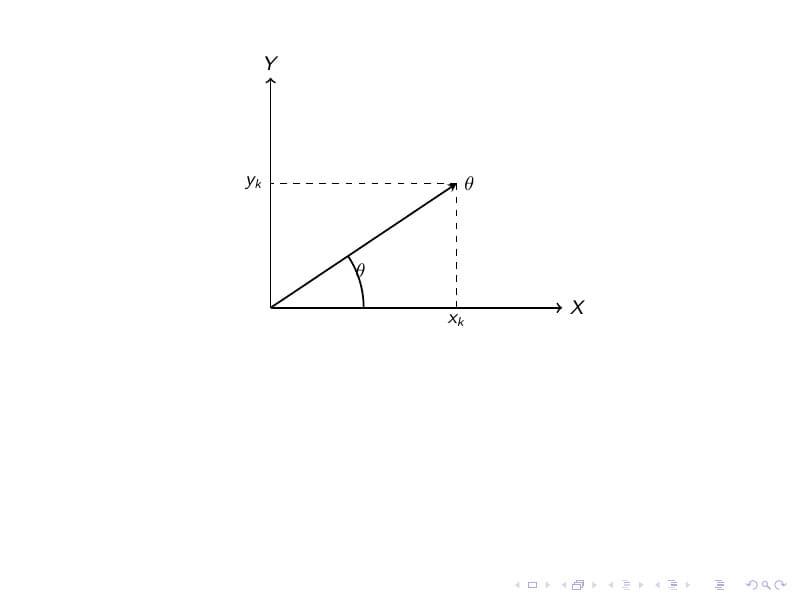
Angle measurement standard deviation

\begin
Discover why over 25 million people worldwide trust Overleaf with their work.

\begin
Discover why over 25 million people worldwide trust Overleaf with their work.
\documentclass[compress,9pt]{beamer}
\usepackage{tikz} %TikZ is required for this to work. Make sure this exists before the next line
\begin{document}
\begin{frame}[fragile]{}
\begin{figure}[H]
%\centering
%\resizebox{0.5\textwidth}{!}{}
\begin{tikzpicture}
\def \accX {3}
\def \accY {2}
\def \sigmaAccX {1}
\def \sigmaAccY {1}
\def \Xaxis {\accX+\sigmaAccX+0.7}
\def \Yaxis {\accY+\sigmaAccY+0.7}
%
% Define angles
% It is very important to get redundant parenthesis
\pgfmathsetmacro{\bottomAngle}{atan(((\accY-\sigmaAccY)) / ((\accX+\sigmaAccX)))}
\pgfmathsetmacro{\mediumAngle}{atan(((\accY)) / ((\accX)))}
\pgfmathsetmacro{\upperAngle}{atan(((\accY+\sigmaAccY)) / ((\accX-\sigmaAccX)))}
%
% Draw coordinate system
\draw[thick,->](0,0) -- (\Xaxis,0) node[right]{$X$};
\draw[thick,->](0,0) -- (0,\Yaxis) node[above]{$Y$};
%
% Draw arrow medium position
\draw[thick,-stealth](0,0) -- (\accX,\accY) node[right]{$\theta$};
% Draw medium point
\draw[dashed] (\accX,\accY) -- (\accX,0) node[below] {$x_k$};
\draw[dashed] (\accX,\accY) -- (0,\accY) node[left] {$y_k$};
% Draw angle
\def \radiusMediumAngle {1.5}
\draw[thick,black] ([shift=(0:\radiusMediumAngle)]0,0) arc (0:\mediumAngle:\radiusMediumAngle)node[below right]{$\theta$};
\pause
% Draw horizontal SD
\draw[dotted] (\accX+\sigmaAccX,\accY-\sigmaAccY) -- (\accX+\sigmaAccX,0) node[rotate=90,left]{$(x_k+\sigma_x)$};
\node[rotate=90,left] at (\accX-\sigmaAccX,0) {$(x_k-\sigma_x)$};
\pause
% Draw vertical SD
\node[left] at (0,\accY-\sigmaAccY) {$(y_k-\sigma_y)$};
\draw[dotted] (\accX-\sigmaAccX,\accY+\sigmaAccY) -- (0,\accY+\sigmaAccY) node[left]{$(y_k+\sigma_y)$};
\pause
% Draw arrow bottom position
\draw[-stealth,blue](0,0) -- (\accX+\sigmaAccX, \accY-\sigmaAccY) node[right]{$(\theta-\sigma_{\theta -})$};
% Angle. Syntax: (startingPointX,startingPointY) arc (startAngle:stopAngle:radius)
% ([shift=(t:r)] x, y) is the proper starting point, where (x,y) is the center and (t:r) is the polar coordinate of starting point.
\def \radiusBottomAngle {2.5}
\draw[thick,blue] ([shift=(\bottomAngle:\radiusBottomAngle)]0,0) arc (\bottomAngle:\mediumAngle:\radiusBottomAngle)node[below right]{$\sigma_{\theta -}$};
\pause
% Draw arrow upper position
\draw[-stealth,red](0,0) -- (\accX-\sigmaAccX, \accY+\sigmaAccY) node[right]{$(\theta+\sigma_{\theta +})$};
% Angle
\def \radiusUpperAngle {2.6}
\draw[thick,red] ([shift=(\mediumAngle:\radiusUpperAngle)]0,0) arc (\mediumAngle:\upperAngle:\radiusUpperAngle)node[right]{$\sigma_{\theta +}$};
\end{tikzpicture}
\end{figure}
\onslide<6->{
\begin{equation}
(\theta_z - \sigma_{\theta -}) = \arctan \frac{y_k-\sigma_y}{x_k+\sigma_x}
,\quad
(\theta_z + \sigma_{\theta +}) = \arctan \frac{y_k+\sigma_y}{x_k-\sigma_x}
\end{equation}}
\onslide<7->{
\begin{equation}\label{eq:sigmaPlusMinus}
\sigma_k =(\sigma_{\theta +} + \sigma_{\theta -}) = \arctan \frac{y_k+\sigma_y}{x_k-\sigma_x} - \arctan \frac{y_k-\sigma_y}{x_k+\sigma_x}
\end{equation}
}
\end{frame}
\end{document}