Geometría Analítica
Forfatter
CARLOS RODRÍGUEZ JASO
Sidst opdateret
7 år siden
Licens
Creative Commons CC BY 4.0
Resumé
Geometría Analítica
Geometría Analítica
% Template created by Karol Kozioł (www.karol-koziol.net) for ShareLaTeX
\documentclass[a4paper,spanish,9pt]{extarticle}
\usepackage[utf8]{inputenc}
\usepackage[T1]{fontenc}
\usepackage{verbatim}
\usepackage{graphicx}
\usepackage{xcolor}
\usepackage{pgf,tikz}
\usepackage{mathrsfs}
\usetikzlibrary{shapes, calc, shapes, arrows, babel}
\usepackage{amsmath,amssymb,textcomp}
\everymath{\displaystyle}
\usepackage{times}
\renewcommand\familydefault{\sfdefault}
\usepackage{tgheros}
\usepackage[defaultmono,scale=0.85]{droidmono}
\usepackage{multicol}
\setlength{\columnseprule}{0pt}
\setlength{\columnsep}{20.0pt}
\usepackage[utf8]{inputenc}
\usepackage[spanish]{babel}
\usepackage{eurosym}
\usepackage{graphicx}
\graphicspath{{./img/}}
\usepackage{svg}
\usepackage{hyperref}
\usepackage{geometry}
\geometry{
a4paper,
total={210mm,297mm},
left=10mm,right=10mm,top=10mm,bottom=15mm}
\linespread{1.3}
\newcommand{\samedir}{\mathbin{\!/\mkern-5mu/\!}}
% custom title
\makeatletter
\renewcommand*{\maketitle}{%
\noindent
\begin{minipage}{0.6\textwidth}
\begin{tikzpicture}
\node[rectangle,rounded corners=6pt,inner sep=10pt,fill=blue!50!black,text width= 0.95\textwidth] {\color{white}\Huge \@title};
\end{tikzpicture}
\end{minipage}
\hfill
\begin{minipage}{0.35\textwidth}
\begin{tikzpicture}
\node[rectangle,rounded corners=3pt,inner sep=10pt,draw=blue!50!black,text width= 0.95\textwidth] {\begin{tabular}{cc} \multirow{2}{1cm}{\includegraphics[width=0.15\columnwidth]{header_right}}& \@author \\ & \ies \end{tabular}};
\end{tikzpicture}
\end{minipage}
\bigskip\bigskip
}%
\makeatother
% custom section
\usepackage[explicit]{titlesec}
\newcommand*\sectionlabel{}
\titleformat{\section}
{\gdef\sectionlabel{}
\normalfont\sffamily\Large\bfseries\scshape}
{\gdef\sectionlabel{\thesection\ }}{0pt}
{
\noindent
\begin{tikzpicture}
\node[rectangle,rounded corners=3pt,inner sep=4pt,fill=blue!50!black,text width= 0.95\columnwidth] {\color{white}\sectionlabel#1};
\end{tikzpicture}
}
\titlespacing*{\section}{0pt}{15pt}{10pt}
% custom footer
\usepackage{fancyhdr}
\makeatletter
\pagestyle{fancy}
\fancyhead{}
\fancyfoot[C]{\footnotesize \@author \ - \ies}
\renewcommand{\headrulewidth}{0pt}
\renewcommand{\footrulewidth}{0pt}
\makeatother
\usepackage{multirow} % para las tablas
\title{Geometría Analítica}
\author{Departamento de Matemáticas}
\date{2014}
\newcommand{\ies}{IES Pedro Cerrada}
\begin{document}
\maketitle
\begin{multicols*}{2}
\section{Vectores Libres}
Dados dos puntos en el plano (A y B, podemos trazar una flecha que vaya del primero al segundo. A esta flecha la llamaremos vector (fijo) y se denota $\overrightarrow{AB}$ o $\overrightarrow{v}$.
\begin{tikzpicture}[scale=0.75]
\coordinate (A) at (1,2);
\coordinate (B) at (6,4);
\draw [fill=blue] (A) circle (2pt) node [left] {A};
\draw [fill=blue] (B) circle (2pt) node [left] {B};
\draw [->, red, thick] (A) -- node[below] {$\overrightarrow{AB}$} (B);
\end{tikzpicture}
\begin{itemize}
\item \textbf{Módulo}: La longitud del vector
\item \textbf{Dirección}: La recta que contiene al vector y cualquiera de sus paralelas
\item \textbf{Sentido}: El que va del origen al final o su contrario. Viene representado por punta "la cabeza de la flecha"
\end{itemize}
Dos vectores (fijos) son \textbf{equipolentes} cuando tienen el mismo módulo, misma dirección y mismo sentido. Un vector fijo y todos sus equipolentes forman lo que de denomina un \textbf{vector libre}. Un vector libre viene determinado por sus coordenadas:
\section{Coordenadas y módulo de un vector} Un vector se puede ver como el desplazamiento que tenemos que hacer horizontalmente y verticalmente para ir del origen al extremo del mismo. Al desplazamiento horizontal le llamaremos primera coordenada y al vertical, segunda.
\begin{itemize}
\item Dados $A(x_1,y_2),B(x_2,y_2) \to \overrightarrow{AB}(x_2-x_1,y_2-y_1)$
\item A partir de las coordenadas del punto podremos calcular su módulo. Dados $\overrightarrow{u}(x,y), \to \left|\overrightarrow{u}\right|=\sqrt{x^2+y^2}$
\end{itemize}
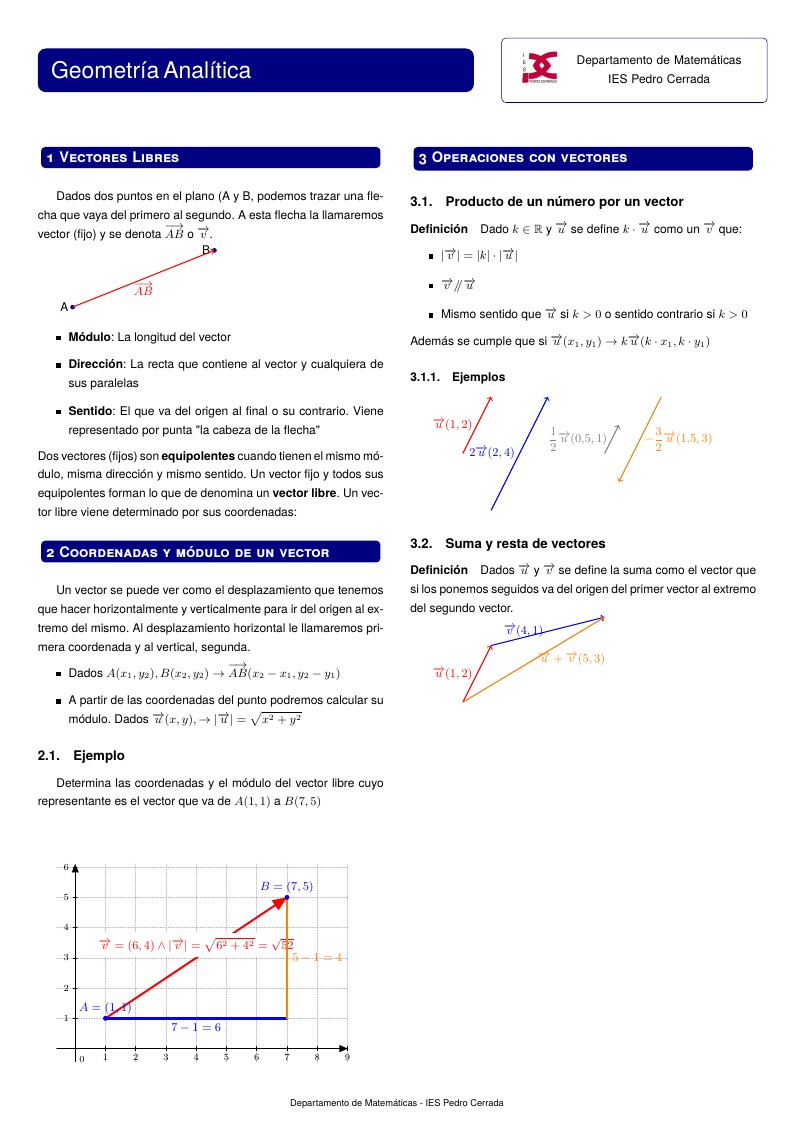
\subsection{Ejemplo}
Determina las coordenadas y el módulo del vector libre cuyo representante es el vector que va de $A(1,1)$ a $B(7,5)$
\begin{tikzpicture}[line cap=round,line join=round,>=triangle 45,x=1cm,y=1cm, scale=0.8]
\draw [color=lightgray,dash pattern=on 1pt off 1pt, xstep=1cm,ystep=1cm] (-0.6129302567150502,-0.43158220601634095) grid (9.010648940148005,6.1);
\draw[->,color=black] (-0.6129302567150502,0) -- (9.010648940148005,0);
\foreach \x in {,1,2,3,4,5,6,7,8,9}
\draw[shift={(\x,0)},color=black] (0pt,2pt) -- (0pt,-2pt) node[below] {\footnotesize $\x$};
\draw[->,color=black] (0,-0.43158220601634095) -- (0,6.1);
\foreach \y in {,1,2,3,4,5,6}
\draw[shift={(0,\y)},color=black] (2pt,0pt) -- (-2pt,0pt) node[left] {\footnotesize $\y$};
\draw[color=black] (0pt,-10pt) node[right] {\footnotesize $0$};
\clip(-0.6129302567150502,-0.43158220601634095) rectangle (9.010648940148005,7.8783927087822985);
\draw [->,line width=1.5pt,color=red] (1,1) -- node[above,fill=white]{$\overrightarrow{v}=\left(6,4 \right) \land \left|\overrightarrow{v}\right|=\sqrt{6^2+4^2}=\sqrt{52}$} (7,5);
\draw [-,line width=2pt,color=blue] (1,1) -- node[below]{$7-1=6$} (7,1);
\draw [-,line width=2pt,color=orange] (7,1) -- node[right]{$5-1=4$}(7,5);
\draw [fill=yellow, color=blue] (1,1) circle (2pt) node[above] {$A = (1, 1)$};
\draw [fill=yellow, color=blue] (7,5) circle (2pt) node[above] {$B = (7, 5)$};
\end{tikzpicture}
\section{Operaciones con vectores}
\subsection{Producto de un número por un vector}
\paragraph*{Definición}
Dado $k \in \mathbb{R}$ y $\overrightarrow{u}$ se define $k\cdot\overrightarrow{u}$ como un $\overrightarrow{v}$ que:\begin{itemize}
\item $\left|\overrightarrow{v}\right|=\left|k\right|\cdot\left|\overrightarrow{u}\right|$
\item $ \overrightarrow{v}\samedir\overrightarrow{u}$
\item Mismo sentido que $\overrightarrow{u}$ si $k>0$ o sentido contrario si $k>0$
\end{itemize}Además se cumple que si $\overrightarrow{u}(x_1,y_1)\to k\overrightarrow{u}(k\cdot x_1,k\cdot y_1)$
\subsubsection{Ejemplos}\begin{tikzpicture}[scale=0.75]
\draw [->, red, thick, fill=red] (1,1) -- node[left] {$\overrightarrow{u}(1,2)$} (2,3);
\draw [->, blue, thick, fill=blue] (2,-1) -- node[left] {$2\overrightarrow{u}(2,4)$} (4,3);
\draw [->, gray, thick, fill=blue] (6,1) -- node[left] {$\frac{1}{2}\overrightarrow{u}(0.5,1)$} (6.5,2);
\draw [->, orange, thick, fill=blue] (8,3) -- node[right] {$-\frac{3}{2}\overrightarrow{u}(1.5,3)$} (6.5,0);
\end{tikzpicture}
\subsection{Suma y resta de vectores}
\paragraph*{Definición} Dados $\overrightarrow{u}$ y $\overrightarrow{v}$ se define la suma como el vector que si los ponemos seguidos va del origen del primer vector al extremo del segundo vector.
\begin{tikzpicture}[scale=0.75]
\draw [->, red, thick, fill=red] (1,0) -- node[left] {$\overrightarrow{u}(1,2)$} (2,2);
\draw [->, blue, thick, fill=blue] (2,2) -- node[left] {$\overrightarrow{v}(4,1)$} (6,3);
\draw [->, orange, thick, fill=blue] (1,0) -- node[right] {$\overrightarrow{u}+\overrightarrow{v}(5,3)$} (6,3);
\end{tikzpicture}
\end{multicols*}
\end{document}